for i in range(n):
for j in range(n):
print('hello n^2')위 코드는 얼마나 복잡한가? 내가 짠 코드나 알고리즘이 얼마나 복잡한지, 또는 시간이 얼마나 걸리는지를 나타내는 지표가 있을까? 있다. 그것이 바로 시간 복잡도(Time Complexity)이다.
시간 복잡도를 나타내는 방법은 Big-O, Omega, Theta가 있다. 그중에서 특히 Big-O는 시간 복잡도의 상한을 나타내기 때문에, 결국 코드의 최소 실행시간보다는 최대 실행시간이 얼마인지 더 중요하다는 점에서 알고리즘의 시간 복잡도의 대표적인 지표로 사용한다. 그에 대해 간단히 알아보자.
Big-O(O)
Big-O는 어떤 알고리즘 식의 최고 차수의 상한(점근적 상한, Asymptotic Upper Bound)을 의미한다. 위 예제에서 코드는 n에 대해 n2번의 계산을 수행한다고 할 수 있다. 이를 식으로는 f(n) = n2로 나타낼 수 있고, Big-O는 해당 식이 가질 수 있는 가장 큰 복잡도 차수를 의미한다. 따라서 O(f(n)) = O(n2)이다. Big-O는 차수의 상한을 나타내는 것이므로, 만일 f(n) = 3n2 + 4n + 2 라고 해도 O(f(n)) = O(n2)으로 나타낼 수 있다. 이를 수학적으로 설명하자면,
n >= n0를 만족하는 모든 n에 대해 f(n) <= c*g(n)을 만족하는 두 양의 상수 c와 n0가 존재할 경우 f(n)의 시간 복잡도는 O(g(n))이다.
위와 같다. 이를 예를 들어 자세히 설명해보자면,
f(n) = 3n2 + 4n + 2 -> 빨간 그래프
g(n) = n2 -> 초록 그래프
라고 할 때,
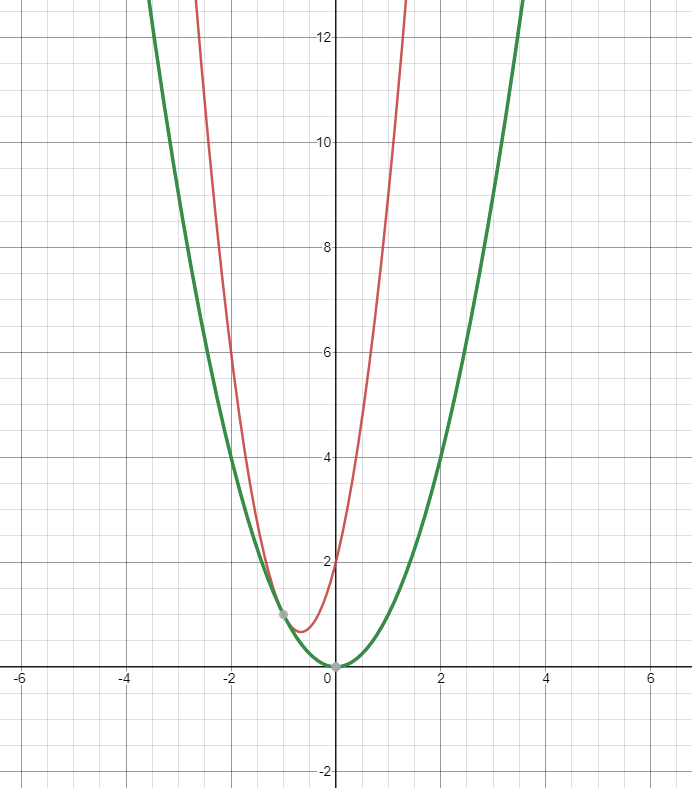
위 이미지와 같은 그래프가 되는데, 이때 상수 c를 9라고 하면
f(n) = 3n2 + 4n + 2
c * g(n) = 9 * n2

위와 같은 그래프가 되고, 그래프를 참고하면 n이 1 이상일 때 f(n) <= c * g(n)이다. 즉, n >= 1(n0) 일 때, f(n) <= c*g(n)을 만족하는 상수 c(=9)가 존재한다는 조건을 만족하므로 f(n)의 시간 복잡도는 O(g(n))이다.
또한 최고 차수의 상한, 즉 이거 보다는 코드 복잡도가 같거나 낮을 거야!라고 말하는 지표이므로 f(n) = n2식에 대해 f(n)의 시간 복잡도를 O(n4)이라 해도 틀린 것은 아니지만, 해당 코드의 복잡도는 O(n2)으로 보는 것이 가장 적절하다고 할 수 있다.
이런 점을 종합해, O(3n2 + 4n + 2)같은 경우 다른 불필요한 것들을 떼어내고 가장 높은 차수만 표현하도록 O(n2)으로 나타내는 것이 일반적이다.
Omega(Ω)
Omega는 Big-O와는 반대되는 개념으로, 어떤 식의 최고 차수의 하한(점근적 하한, Asymptotic Lower Bound)을 의미한다. 즉, 이 코드는 최소 이것 이상으로는 복잡할 거야!라고 말하는 지표이다. 이를 수학적으로 설명하면,
n >= n0를 만족하는 모든 n에 대해 f(n) >= c*g(n)을 만족하는 두 양의 상수 c와 n0가 존재할 경우 f(n)의 시간 복잡도는 Ω(g(n))이다.
위와 같다. f(n) = 3n2 + 4n + 2라고 하면, 최고 차수인 n2보다 같거나 낮은 것은 모두 해당한다. 즉 Ω(n2)은물론이고, Ω(n), Ω(1)도 모두 성립한다.
위 Big-O에서 들었던 예를 다시 다시 가져와 설명하자면, 만약 g(n)의 최고 차수가 예를 들어 n의 3승 이상일 경우, 즉 f(n)의 최고 차수인 n의 2승보다 높을 경우 g(n)에 그 어떤 양의 상수를 곱한다 해도 특정 n 이상의 수에서 항상 f(n) >= c * g(n)을 만족하는 경우는 없으므로, Ω(n2)을 초과하는 것은 답이 될 수 없다. 반대로, g(n) = 1 등 상수의 경우 특정 양의 수 n 이상에서 f(n) >= c * g(n)을 만족하는 양의 상수 c가 존재하므로 Ω(1)같은 경우는 f(n)에 대해 성립한다고 할 수 있다.
Theta(Θ)
Theta는 Big-O와 Omega를 모두 만족하는 일종의 교집합(Asymptotically Tight Bound)이다. 달리 말해, f(n) = 3n2 + 4n + 2일 때 O(f(n))으로 가능한 것은 O(n2) 이상, Ω(f(n))으로 가능한 것은 Ω(n2) 이하이므로, 이 둘의 교집합인 n2이 Theta로 가능한 것이다. 즉, f(n)의 Theta는 Θ(n2)으로 나타낼 수 있다. 이러한 점을 수학적으로 설명하면,
n >= n0를 만족하는 모든 n에 대해 c1*g(n) <= f(n) <= c2*g(n)을 만족하는 양의 상수 c1, c2와 n0가 존재할 경우 f(n)의 시간 복잡도는 Θ(g(n))이다.
위와 같다. 이를 자세히 설명해보면,
f(n) = 3n2 + 4n + 2 -> 빨간색
g(n) = n2
c1 = 1, c1 * g(n) -> 보라색
c2 = 9, c2 * g(n) -> 초록색

이렇게 f(n)과 g(n)에 대해 n은 1이상에서 c1 = 1, c2 = 9일 때, c1 * g(n) <= f(n) <= c2 * g(n)을 만족한다. 따라서 f(n)의 Theta는 n2이라고 할 수 있다.
이는 가장 정확하게 알고리즘 시간복잡도를 나타내는 표현법이지만, 최악의 경우를 나타내는 Big-O가 가장 일반적으로 사용된다.
추가로, log에 대한 시간 복잡도 표현은 통상적으로 O(logn)으로 표현하는데, log의 밑x가 무엇이 되든 특정 n이상에서 logxn <= clogn을 만족하는 상수 c가 존재할 수 있기 때문이다.


'컴퓨터 공학(Computer Engineering) > 자료구조(Data Structure)' 카테고리의 다른 글
| 떡국 = (떡국떡)국 = ((떡국떡)국떡)국... [재귀프로그램] (0) | 2021.04.03 |
|---|---|
| 65 83 67 73 73, 이것은 컴퓨터의 글자다. [컴퓨터의 숫자와 문자 표현] (1) | 2021.04.03 |
| 500GB짜리 용량의 디스크가 실제로 500GB가 아닌 이유? [자료구조의 개념과 단위] (0) | 2021.04.02 |

